Реферат: Функціональний ряд, область його збіжності. Cтепеневі ряди. Теорема Абеля

План

Функціональний ряд.

Область збіжності

Рівномірна збіжність

Степеневі ряди

Теорема Абеля

Інтервал і радіус збіжності степеневого ряду

Ряди за степенями

1. Функціональні ряди

1.1. Функціональні ряди. Область збіжності

Ряд

(13.22)

називається функціональним, якщо його члени є функціями від Надаючи певного числового значення, ми одержимо різні числові ряди. Одні з них можуть бути збіжними, інші – розбіжними.

Означення. Сукупність тих значень при яких ряд (13.22) збігається, називається областю збіжності функціонального ряду.

Очевидно, що в області збіжності ряду його сума є деякою функцією від . Тому його суму будемо позначати через

Через позначимо частинну суму ряду (13.22), тобто суму перших його членів

(13.23)

Тоді

, (13.24)

де

і називається залишком ряду. Для всіх значень в області збіжності ряду має місце співвідношення а тому

(13.25)

тобто залишок збіжного ряду прямує до нуля при

Приклад. Знайти область збіжності ряду .

Р о з в ‘ я з о к. Для знаходження області збіжності даного функціонального ряду використаємо радикальну ознаку Коші

. Ряд збігається при тих

значеннях при яких ця границя менша за одиницю, тобто

Дослідимо збіжність ряду на кінцях проміжку, тобто при і .

При : ряд розбігається.

При : ряд розбігається.

Областю збіжності даного ряду є проміжок

1.2. Рівномірна збіжність

Означення. Функціональний ряд (13.22), збіжний для всіх із області , називається рівномірно збіжним в цій області, якщо для довільного як завгодно малого числа існує такий незалежний від номер що при нерівність

або (13.26)

виконується одночасно для всіх із

Приклад 1. Розглянемо прогресію

вона збігається в відкритому проміжку Для довільного із залишок ряду має вигляд:

Якщо довільно зафіксувати, то, очевидно:

Це показує, що здійснити для всіх одночасно нерівність

(якщо )

при одному й тому ж номері неможливо. Отже, збіжність прогресії

в проміжку нерівномірна; це ж відноситься і до проміжків і зокрема.

Приведемо без доведення ознаку рівномірної збіжності ряду (13.22).

Ознака рівномірної збіжності. Для того, щоби ряд (13.22) рівномірно збігався в області необхідно і достатньо, щоби для кожного числа існував такий не залежний від номер що при і довільному нерівність

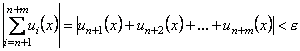(13.27)

буде мати місце для всіх із одночасно.

Для встановлення на практиці рівномірної збіжності рядів користуються більш зручнішими в застосуванні достатніми ознаками, наприклад ознакою Вейєрштрасса.

Ознака Вейєрштрасса. Якщо члени функціонального ряду (13.22) задовольняють в області нерівностям

(13.28)

і числовий ряд

(13.29)

збігається, то ряд (13.22) збігається в рівномірно.

При наявності нерівності (13.28) говорять, що ряд (13.22) мажорується рядом (13.29), або що ряд (13.29) служить мажорантним рядом для (13.22).

Приклад 2. Розглянемо ряд

Р о з в ‘ я з о к. Оскільки нерівності виконуються на всій числовій осі, а числовий ряд збігається, то даний функціональний ряд рівномірно збігається на

1.3. Функціональні властивості суми ряду

Ми переходимо тепер до вивчення функціональних властивостей суми ряду, складеного із функцій, в зв’язку із властивістю останніх.

Cума скінченого числа неперервних на відрізку функцій є неперервна на цьому відрізку функція. Для суми ряду (що складається із безмежного числа доданків) ця властивість не зберігається. Тут необхідні додаткові вимоги на неперервні доданки.

Теорема 1 (про неперервність суми ряду). Якщо функції визначені та неперервні в проміжку і ряд (13.22) рівномірно збігається в до суми , то й ця сума буде неперервною в проміжку

Зауваження. Рівномірна збіжність фігурує в теоремі лише як достатня умова і не потрібно думати, що ця умова є необхідною для неперервності суми ряду. Наприклад, ряд

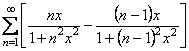
на відрізку має неперервну суму, тотожньо рівну нулю, хоча на цьому відрізку ряд збігається нерівномірно.

Теорема 2 (про почленний перехід до границі). Нехай кожна з функцій визначена в області і має скінченну границю при :