Реферат: Інвестиції і інвестиційна діяльність. Економічна суть інвестицій

Приклад 4. Інвестування в випуск нової техніки (випуск літаків).

1.4. Динамічні ендогенні моделі та методи оптимізації інвестицій у двосекторній економіці

Одним з важливих питань сучасної економічної теорії є дослідження ролі інновацій та науково-дослідної діяльності в процесі економічного розвитку суспільства. Д.Шумпетер першим розглянув еволюційний підхід в економічному аналізі і вважав, що ”якщо система і може досягти рівноваги, саме інновації (привнесені діяльністю підприємців) призводять до її порушення та сприяють еволюції економіки" [1]. Пізніше теорія інноваційних змін була розроблена в рамках мікроекономічного аналізу, але з появою в 6О-ті роки динамічних моделей економічного зростання еволюційний підхід Д.Шумпетера став все більш застосовуватись в макроекономіці [2].

На сьогодні це питання стоїть на перехресті двох теорій математичної економіки, а саме, сучасних мікроекономічної та макроекономічної теорій. При математичному моделюванні мікроекономічного підходу такі показники, як ринкові умови, ступінь конкуренції, інноваційна діяльність інших фірм, обмежений характер застосування базових знань або ж і самого продукту інноваційної діяльності задаються параметрично. Сучасні мікроекономічні моделі підкреслюють важливість зворотних зв'язків між діяльністю економічних суб'єктів, але така діяльність на рівні окремо розглянутих виробників ще не змінює параметрів стану загальної економічної структури. Це суттєво відрізняє мікроекономічний підхід від макроекономічного.

Макроекономічний аналіз базується на агрегованому підході, який висвітлює динаміку зростання економічної системи в цілому і дає можливість проаналізувати аспекти державної політики, такі, як фіскальна політика, питання оптимального розподілу капіталовкладень, тощо. На макроекономічному рівні інновації надається роль двигуна в економічному зростанні суспільства. Саме завдяки інноваційній діяльності економіка відходить від свого рівноважного стану, сприяючи економічному розвитку. Останній може бути зображений як циклічний рух від рівноваги, яка склалася, до порушення її і далі до формування на більш високому рівні нової рівноваги більш складного порядку.

Сучасні економічні теорії роблять спробу поєднати відому теорію бізнес циклів [3] та теорію технічного прогресу, який призводить до революційних стрибків в економічному розвитку, в єдину теорію економічних флуктуацій. Відомо, що якщо економічні суб'єкти в періоди економічних ”бумів” вкладають більші кошти на накопичення капіталу, який можна використати в періоди спадів в економіці, то така поведінка згладжує функцію коливань. Стабілізаційна політика в цьому випадку зводиться до регулювання процесу накопичення методами фіскальної політики. Аналогічно, фіскальна політика, яка стимулює вкладання коштів у науково-технічну діяльність, повинна забезпечувати стійкість процесу економічного зростання.

Беручи до уваги перспективність такого комплексного підходу, можна зрозуміти необхідність знаходження закономірностей, які діють в економічній системі, якщо розвиток останньої відбувається насамперед завдяки внутрішній науково-технічній діяльності.

Метою доповіді є формалізація моделей ендогенного зростання в двосекторній економіці завдяки розробкам наукового сектора та дослідження оптимальної стратегії фіскальної політики для фінансування громадських інвестицій в наукову та інноваційну сфери на базі застосування методів оптимізації.

Математична модель. Розглядається умовна двосекторна економіка, де роль центру виконує деякий усереднений споживач, який є власником трудових ресурсів, що задаються константою , та капітальних ресурсів і займається їх раціональним розподілом між секторами. В моделі всі змінні є функціями часу (далі в тексті ця залежність може не записуватись, окрім випадків, де на це потрібно наголосити).

Перший сектор виробляє продукцію , частина якої є продукцією споживання , а інша частина йде на інвестиції . Випуск продукції здійснюється за виробничою функцією

(1)

де та є відповідно трудо- та капіталовкладення в першому виробничому секторі.

Другий сектор відповідає за інтелектуальну продукцію , створення якої відбувається за виробничою функцією

, (2)

де та є відповідно трудо- та капіталовкладення в другому секторі. Параметри та в формулах (1) і (2) відповідають за продуктивність секторів, а є функцією, що відповідає за технологічний рівень розглянутого виробництва.

Виробничі функції в (1), (2) задаються відомою в економіці формою Коба-Дугласа [5]. Така функція є двічі неперервно- диференційованою, опуклою вверх І зростаючою за кожним з аргументів. На границях перші похідні прямують до нескінченності, якщо аргументи прямують до нуля, і до нуля, якщо аргументи прямують до нескінченності. Кожен з аргументів є важливим для виробництва:

функція набуває нульового значення, якщо хоча б один з аргументів дорівнює нулю. Для існування сталого стану доведено, що функція технологічних змін має бути записана у формі множника до аргументу [2].

Розглянемо задачу центру, яка полягає в максимізації функції корисності на проміжку всього часу існування (за припущенням, нескінченного):

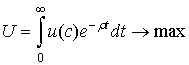(3 )

де функція корисності має вигляд

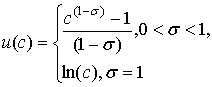(4)

є параметром еластичності споживання за часом, а - фактор знецінення. Максимізація (3) ведеться з врахуванням динамічної умови

( 5 )

що задає обмеження на фінансові активи споживача, які складаються з процентної ставки на попередні капіталовкладення, та заробітної плати , за винятком затрат на споживання .

Для розв'язку задачі центру (З), (5) використовується принцип максимуму і знаходиться така функція швидкості економічного зростання:

(6)

Функція ( 6 ) задає значення для швидкості зростання змінних та в точці сталого стану в задачі оптимального розподілу ресурсів між виробничим та науковим секторами. Ця задача полягає в максимізації критерію (3) за законами динамічної зміни та :

(7)

( 8 )

і за обмеженнями на трудо- та капіталоресурси вигляду:

, (9)

, (10)

де та - трудові ресурси, а та -капітальні ресурси, задіяні відповідно в першому та другому секторах.

Для підзадачі (З),(7)-(10) виписується гамільтоніан, який диференціюється за змінними стану та керування за стандартним алгоритмом, і задача оптимізації зводиться до системи диференційних рівнянь. В точці сталого стану, коли всі змінні стану економіки зростають з однаковою оптимальною швидкістю [4] , задача зводиться до системи звичайних нелінійних рівнянь відносно змінних та , яка розв'язується числовими методами.