Реферат: Рух небесних тіл під дією сил тяжіння

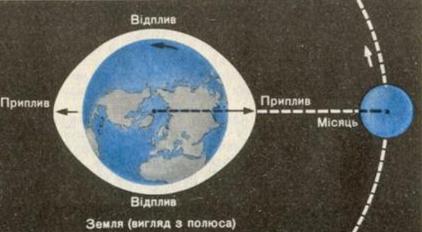
Мал.2. Схема місячних припливів

6. Визначення мас небесних тіл. Ньютон довів, що точнішою є така формула третього закону Кеплера:

де М1 і М2 — маси будь-яких небесних тіл, а m1 і m2 — відповідно маси їхніх супутників. Так, планети є супутниками Сонця. Ми бачимо, що уточнена формула цього закону відрізняється від наближеної наявністю множника, який містить маси. Якщо під М1 = М2 = МÅ розуміти масу Сонця, а під m1 і m2 — маси двох різних планет, то відношення мало відрізнятиметься від одиниці, бо m1 і m2 дуже малі порівняно з масою Сонця. При цьому точна формула помітно не відрізнятиметься від набли­женої.

Уточнений третій закон Кеплера дає змогу визначити маси планет, які мають супутників, і масу Сонця. Щоб визначити масу Сонця, порівняємо рух Місяця навколо Землі з рухом Землі навколо Сонця:

де TÅ і аÅ — період обертання Землі (рік) і велика піввісь її орбіти, Tc і ас— період обертання Місяця навколо Землі і велика піввісь його орбіти, М¤ — маса Сонця, МÅ — маса Землі, mc — маса Місяця. Маса Землі дуже незначна порівняно з масою Сон­ця, а маса Місяця мала (1 : 81) порівняно з масою Землі. Тому другі доданки в сумах можна відкинути, не роблячи великої

похибки. Розв'язавши рівняння відносно маємо:

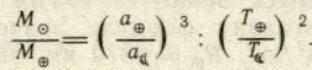
Ця формула дає змогу визначати масу Сонця, виражену в ма­сах Землі. Вона становить близько 333000 мас Землі.

Для порівняння мас Землі та іншої планети, наприклад Юпі­тера, треба у вихідній формулі індекс 1 віднести до руху Місяця навколо Землі масою M1, а 2 — до руху будь-якого супутника навколо Юпітера масою M2.

Маси планет, що не мають супутників, визначають за тими збуреннями, які вони спричиняють своїм притяганням у русі сусід­ніх з ними планет, а також у русі комет, астероїдів чи космічних апаратів.