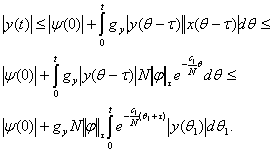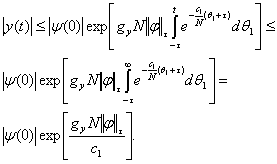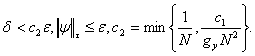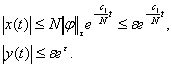1. Вступ У багатьох застосуваннях припускається, що на поведінку піддослідної системи не впливає жодна затримка в часі, тобто майбутній стан системи не залежить від попередніх станів і визначається лише теперішнім. У таких випадках динамічна система переважно моделюється звичайними диференціальними рівняннями. Однак при глибшому вивченні виявляється, що такий погляд – це лише перше наближення до дійсного стану і реальніша модель повинна включати минулі стани системи. Крім того, деякі задачі повністю втрачають свій зміст без розгляду “попередньої історії”. Ці положення були відомі й раніше, але теорія систем з післядією інтенсивно розвивається лише протягом останніх 50 років. Досягнення в галузі обчислювальної техніки є дуже важливими, оскільки теорія інтегрування, тобто аналітичного розв’язування, для систем з післядією не настільки успішна. Перші системи, з якими зіткнулися дослідники, були біологічними. При дослідженні динаміки популяцій двох антагоністичних видів [7] використовувалися системи із запізненням. Р.Беллман [3] вивчав наслідки введення у кров хімічного розчину. Зауважимо, що рівняння, які описують цей процес, не є звичайними диференціальними рівняннями, оскільки повна циркуляція крові триває близько двох хвилин. Мета цієї праці – проаналізувати систему імунного захисту організму, враховуючи запізнення в часі. Вперше модель імунного захисту людського організму була розроблена групою математиків і лікарів на чолі з Г.І.Марчуком. Як зазначає Г.І.Марчук [1], модель дала непогані результати при використанні її для лікування пневмонії та вірусного гепатиту. 2. Асимптотична стійкість 2.1. Головні результати теорії стійкості Широке коло задач пов’язано з дослідженнями динаміки об’єктів, що описуються диференціальними рівняннями із запізненням: 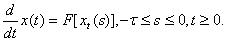  (2.1) (2.1)
Тут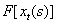 – функціонал, визначений для довільного фіксованого – функціонал, визначений для довільного фіксованого 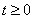 на множині кусково-неперервних функцій: на множині кусково-неперервних функцій: 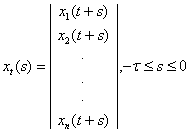
Одним із найзагальніших методів дослідження стійкості таких задач є прямий метод Ляпунова. Використання такої методики для систем із післядією пов’язано з двома напрямками. Перший ґрунтується на скінченно-вимірних функціях Ляпунова і використовує теореми Б.С.Разуміхіна. Однак цей підхід має недолік: не доведено необхідності цих умов стійкості. Сенс диференціально-різницевих рівнянь полягає в нескінченно-вимірних просторах. Використання скінченно-вимірних функцій Ляпунова призводить до зайвих достатніх умов. З цієї причини М.М.Красовський [8] запропонував підійти до вивчення стійкості з точки зору дослідження процесів у функціональних просторах. Як точку простору він запропонував розглядати не вектор 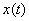 , а вектор-відрізок цієї траєкторії , а вектор-відрізок цієї траєкторії 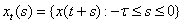 . Замість функції . Замість функції 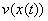 він запропонував використовувати функціонал він запропонував використовувати функціонал 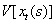 , визначений на відрізку , визначений на відрізку 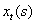 . Використання функціоналів – це природнє узагальнення прямого методу Ляпунова для звичайних диференціальних рівнянь на рівняння із запізненням. Головний результат для автономних систем твердить [2]. . Використання функціоналів – це природнє узагальнення прямого методу Ляпунова для звичайних диференціальних рівнянь на рівняння із запізненням. Головний результат для автономних систем твердить [2]. Теорема 2.1. Нехай існують 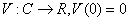 - функціонал і неперервні функції - функціонал і неперервні функції 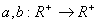 такі, що такі, що 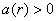 при при 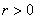 , , 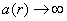 при при 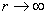 , , 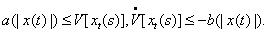
Тоді незбурений роз’язок 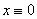 системи (1) є стійким, а кожен роз’язок обмеженим. Якщо, крім цього, системи (1) є стійким, а кожен роз’язок обмеженим. Якщо, крім цього, 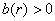 при при 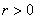 , тоді кожен розв’язок прямує до нуля при , тоді кожен розв’язок прямує до нуля при 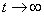 . . 2.2. Один загальний випадок нелінійної системи третього порядку із запізненням Розглянемо систему диференціальних рівнянь із запізненням: 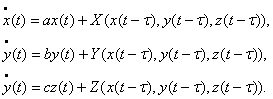 (2.2) (2.2)
Тут 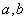 і і 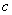 – від’ємні константи, функції – від’ємні константи, функції 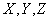 задовольняють наступні умови: задовольняють наступні умови: 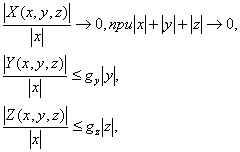 (2.3) (2.3)
де 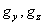 – додатні константи. – додатні константи. Теорема 2.2. Нехай умови (2.3) виконані. Тоді незбурений розв’язок 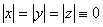 (2.2) є стійким та експоненціально (2.2) є стійким та експоненціально 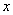 -стійким. -стійким. Доведення. Нехай 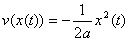 – функція Ляпунова для скалярного рівняння: – функція Ляпунова для скалярного рівняння: 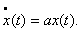 (2.4) (2.4)
Тоді: 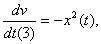 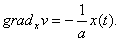
Розглянемо функціонал, що відображає 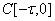 в в 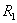 вигляду: вигляду: 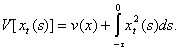
Повна похідна функціоналу вздовж першого рівняння з (2.2) має вигляд: 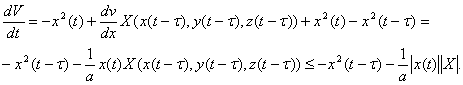
Згідно з умовами (3), існує 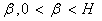 таке, що: таке, що: 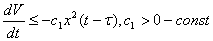 (2.5) (2.5)
у сфері: 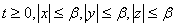 . (2.6) . (2.6)
Функціонал 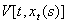 задовольняє умови: задовольняє умови: (2.7) при досить великому N. Нехай 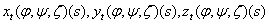 – довільний розв’язок системи (2.2) з початковими умовами – довільний розв’язок системи (2.2) з початковими умовами 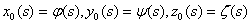 зі сфери: зі сфери: 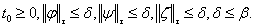
Розглянемо інтервал 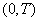 , на якому піддослідний розв’язок зодовольняє умови: , на якому піддослідний розв’язок зодовольняє умови: 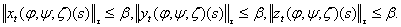
Оскільки мають місце (2.5), (2.6), (2.7), то, як випливає з теореми 2 (див. [10], стор.145), розв’язок першого рівняння з (2.2) – експоненціально x-стійкий, тобто: 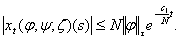 (2.8) (2.8)
Уявимо функцію 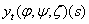 , яка задовольняє друге рівняння з (2.2) у наступному вигляді: , яка задовольняє друге рівняння з (2.2) у наступному вигляді: 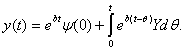 (2.9) (2.9)
Оскільки 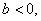 то маємо: то маємо: 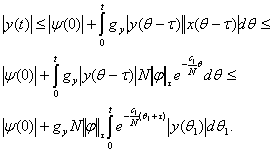
Застосовуючи до останньої нерівності лему Гронуола-Беллмана, отримуємо: 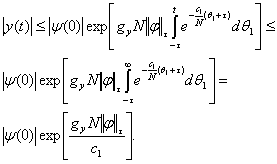
Виберемо 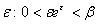 і і 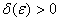 такі, що мають місце нерівності: такі, що мають місце нерівності: 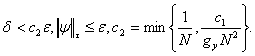
Звідси при 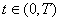 має місце: має місце: 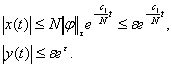
Нехай 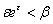 . Таким чином, нерівності мають місце для довільного . Таким чином, нерівності мають місце для довільного 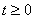 . Таким же чином, як це було зроблено для . Таким же чином, як це було зроблено для 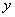 , можна довести , можна довести 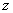 -стійкість (2.2). Теорему доведено. -стійкість (2.2). Теорему доведено.
| 

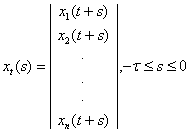
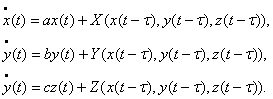 (2.2)
(2.2)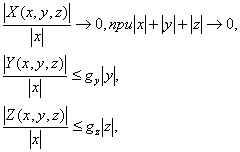 (2.3)
(2.3)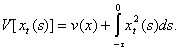
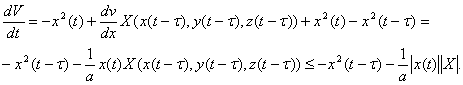
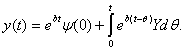 (2.9)
(2.9)