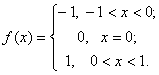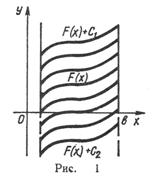  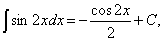 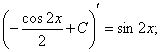
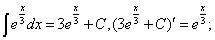
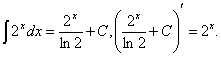
2°. Невизначний Інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої: 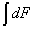 (х) = (х) = 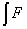 '(х) dx = '(х) dx = 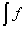 (х) dx = F(х) + С. (х) dx = F(х) + С.
3°. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу: d(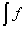 (х) dx) - ( (х) dx) - (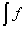 (х) dx)' dx = f(х) dx. (х) dx)' dx = f(х) dx. 4°. Сталий множник можна виносити за знак інтеграла: 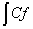 (x)dx=C (x)dx=C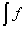 (x)dx. (x)dx.
5°. Невизначений інтеграл від алгебраїчної суми двох функцій дорівнює алгебраїчній сумі інтегралів від цих функцій: 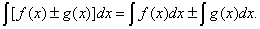
Властивості 4° і 5° перевіряються диференціюванням на основі властивості 1°. Властивість 5° справедлива для довільного скінченного числа доданків. 6°. Якщо 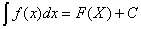
і u =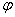 (х) — довільна функція, що має неперервну похідну, то (х) — довільна функція, що має неперервну похідну, то 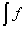 (u)du=F(u)+C. (2) (u)du=F(u)+C. (2)
О Внаслідок інваріантності форми першого диференціала (гл. 5, п. 3.2) і властивості 2° маємо dF (u)=F'(u) du=f(u) du; 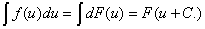
Ця властивість (її називають інваріантністю формули інтегрування) дуже важлива. Вона означає, що та чи інша формула для невизначеного інтеграла залишається справедливою незалежно від того, чи змінна інтегрування є незалежною змінною, чи довільною функцією від неї, що має неперервну похідну. Таким чином, кількість інтегралів, які обчислюються (або, як кажуть, «беруться»), необмежено збільшується. Наприклад, 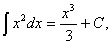 оскільки оскільки 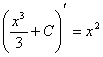 . . Користуючись інваріантністю цієї формули, одержимо формулу 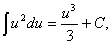 де де 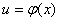 — довільна функція, що має неперервну похідну. Зокрема: — довільна функція, що має неперервну похідну. Зокрема: 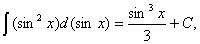
тобто 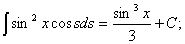 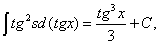
тобто 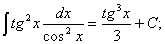 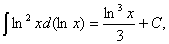
тобто 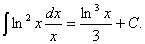 Природно, виникає запитання: чи для всякої функції існує невизначений інтеграл? Негативну відповідь на це запитання дає такий приклад: нехай 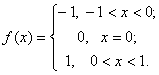
Покажемо, що функція f(x) на проміжку (- 1; 1) не має первісної. Припустимо протилежне. Нехай існує така функція F(х), що 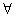 х х 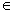 ( - 1; 1): F'(х)=f(х). Тоді з теореми Лагранжа на відрізку [0; х], 0 < x < l, випливає, що ( - 1; 1): F'(х)=f(х). Тоді з теореми Лагранжа на відрізку [0; х], 0 < x < l, випливає, що 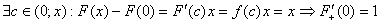
(F'+ (0) — права похідна функції F(х) в точці х = 0). Але F'+ (0) = F(0) = 0. Одержане протиріччя означає, що задана функція первісної не має. Цей приклад показує, що потрібна теорема, яка б гарантувала існування невизначеного інтеграла. В п. 2.4 буде доведено, що всяка неперервна на проміжку 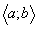 функція має на цьому проміжку первісну. У зв'язку з цим надалі вважатимемо, що підінтегральна функція розглядається дише на тих проміжках, де вона неперервна. функція має на цьому проміжку первісну. У зв'язку з цим надалі вважатимемо, що підінтегральна функція розглядається дише на тих проміжках, де вона неперервна.
| 


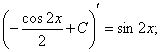
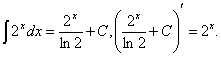
 .
.